Notes

EXAMPLE 1 In the ISQ, the quantity dimension of force is denoted by dim F = LMT^–2.

EXAMPLE 2 In the same system of quantities, dim ρ_B = ML^–3 is the quantity dimension of mass concentration of component B, and ML^–3 is also the quantity dimension of mass density, ρ (volumic mass).

EXAMPLE 3 The period T of a pendulum of length l at a place with the local acceleration of free fall g is

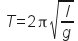or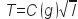

where

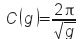
Hence dim C(g) = L^–1/2 T.

NOTE 1 A power of a factor is the factor raised to an exponent. Each factor is the dimension of a base quantity.

NOTE 2 The conventional symbolic representation of the dimension of a base quantity is a single upper case letter in roman (upright) sans-serif type. The conventional symbolic representation of the dimension of a derived quantity is the product of powers of the dimensions of the base quantities according to the definition of the derived quantity. The dimension of a quantity Q is denoted by dim Q.

NOTE 3 In deriving the dimension of a quantity, no account is taken of its scalar, vector, or tensor character.

NOTE 4 In a given system of quantities,

- quantities of the same kind have the same quantity dimension,

- quantities of different quantity dimensions are always of different kinds, and

- quantities having the same quantity dimension are not necessarily of the same kind.

NOTE 5 Symbols representing the dimensions of the base quantities in the ISQ are:

Thus, the dimension of a quantity Q is denoted by dim Q = L^αM^βT^γI^δΘ^εN^ζJ^η where the exponents, named dimensional exponents, are positive, negative, or zero.

1 Quantities and units

• 1.1 quantity
• 1.2 kind of quantity
• 1.3 system of quantities
• 1.4 base quantity
• 1.5 derived quantity
• 1.6 International System of Quantities
• 1.7 quantity dimension
• 1.8 quantity of dimension one
• 1.9 measurement unit
• 1.10 base unit
• 1.11 derived unit
• 1.12 coherent derived unit
• 1.13 system of units
• 1.14 coherent system of units
• 1.15 off-system measurement unit
• 1.16 International System of Units
• 1.17 multiple of a unit
• 1.18 submultiple of a unit
• 1.19 quantity value
• 1.20 numerical quantity value
• 1.21 quantity calculus
• 1.22 quantity equation
• 1.23 unit equation
• 1.24 conversion factor between units
• 1.25 numerical value equation
• 1.26 ordinal quantity
• 1.27 quantity-value scale
• 1.28 ordinal quantity-value scale
• 1.29 conventional reference scale
• 1.30 nominal property

2 Measurement

• 2.1 measurement
• 2.2 metrology
• 2.3 measurand
• 2.4 measurement principle
• 2.5 measurement method
• 2.6 measurement procedure
• 2.7 reference measurement procedure
• 2.8 primary reference measurement procedure
• 2.9 measurement result
• 2.10 measured quantity value
• 2.11 true quantity value
• 2.12 conventional quantity value
• 2.13 measurement accuracy
• 2.14 measurement trueness
• 2.15 measurement precision
• 2.16 measurement error
• 2.17 systematic measurement error
• 2.18 measurement bias
• 2.19 random measurement error
• 2.20 repeatability condition of measurement
• 2.21 measurement repeatability
• 2.22 intermediate precision condition of measurement
• 2.23 intermediate measurement precision
• 2.24 reproducibility condition of measurement
• 2.25 measurement reproducibility
• 2.26 measurement uncertainty
• 2.27 definitional uncertainty
• 2.28 Type A evaluation of measurement uncertainty
• 2.29 Type B evaluation of measurement uncertainty
• 2.30 standard measurement uncertainty
• 2.31 combined standard measurement uncertainty
• 2.32 relative standard measurement uncertainty
• 2.33 uncertainty budget
• 2.34 target measurement uncertainty
• 2.35 expanded measurement uncertainty
• 2.36 coverage interval
• 2.37 coverage probability
• 2.38 coverage factor
• 2.39 calibration
• 2.40 calibration hierarchy
• 2.41 metrological traceability
• 2.42 metrological traceability chain
• 2.43 metrological traceability to a measurement unit
• 2.44 verification
• 2.45 validation
• 2.46 metrological comparability of measurement results
• 2.47 metrological compatibility of measurement results
• 2.48 measurement model
• 2.49 measurement function
• 2.50 input quantity in a measurement model
• 2.51 output quantity in a measurement model
• 2.52 influence quantity
• 2.53 correction

3 Devices for measurement

• 3.1 measuring instrument
• 3.2 measuring system
• 3.3 indicating measuring instrument
• 3.4 displaying measuring instrument
• 3.5 scale of a displaying measuring instrument
• 3.6 material measure
• 3.7 measuring transducer
• 3.8 sensor
• 3.9 detector
• 3.10 measuring chain
• 3.11 adjustment of a measuring system
• 3.12 zero adjustment of a measuring system

4 Properties of measuring devices

• 4.1 indication
• 4.2 blank indication
• 4.3 indication interval
• 4.4 nominal indication interval
• 4.5 range of a nominal indication interval
• 4.6 nominal quantity value
• 4.7 measuring interval
• 4.8 steady-state operating condition
• 4.9 rated operating condition
• 4.10 limiting operating condition
• 4.11 reference operating condition
• 4.12 sensitivity of a measuring system
• 4.13 selectivity of a measuring system
• 4.14 resolution
• 4.15 resolution of a displaying device
• 4.16 discrimination threshold
• 4.17 dead band
• 4.18 detection limit
• 4.19 stability of a measuring instrument
• 4.20 instrumental bias
• 4.21 instrumental drift
• 4.22 variation due to an influence quantity
• 4.23 step response time
• 4.24 instrumental measurement uncertainty
• 4.25 accuracy class
• 4.26 maximum permissible measurement error
• 4.27 datum measurement error
• 4.28 zero error
• 4.29 null measurement uncertainty
• 4.30 calibration diagram
• 4.31 calibration curve

5 Measurement standards (Etalons)

• 5.1 measurement standard
• 5.2 international measurement standard
• 5.3 national measurement standard
• 5.4 primary measurement standard
• 5.5 secondary measurement standard
• 5.6 reference measurement standard
• 5.7 working measurement standard
• 5.8 travelling measurement standard
• 5.9 transfer measurement device
• 5.10 intrinsic measurement standard
• 5.11 conservation of a measurement standard
• 5.12 calibrator
• 5.13 reference material
• 5.14 certified reference material
• 5.15 commutability of a reference material
• 5.16 reference data
• 5.17 standard reference data
• 5.18 reference quantity value