Notes

EXEMPLE 1 Dans l'ISQ, la dimension de la force est notée dim F = LMT^–2.

EXEMPLE 2 Dans le même système de grandeurs, dim ρ_B = ML^–3 est la dimension de la concentration en masse du constituant B, et ML^–3 est aussi la dimension de la masse volumique ρ.

EXEMPLE 3 La période T d'un pendule de longueur l en un endroit où l'accélération locale de la pesanteur vaut g est

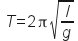ou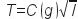

où

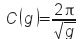
Par conséquent, dim C(g) = L^–1/2 T.

NOTE 1 Une puissance d'un facteur est le facteur muni d'un exposant. Chaque facteur exprime la dimension d'une grandeur de base.

NOTE 2 Par convention, la représentation symbolique de la dimension d'une grandeur de base est une lettre majuscule unique en caractère romain (droit) sans empattement. Par convention, la représentation symbolique de la dimension d'une grandeur dérivée est le produit de puissances des dimensions des grandeurs de base conformément à la définition de la grandeur dérivée. La dimension de la grandeur Q est notée dim Q.

NOTE 3 Pour établir la dimension d'une grandeur, on ne tient pas compte du caractère scalaire, vectoriel ou tensoriel.

NOTE 4 Dans un système de grandeurs donné,

- les grandeurs de même nature ont la même dimension,

- des grandeurs de dimensions différentes sont toujours de nature différente,

- des grandeurs ayant la même dimension ne sont pas nécessairement de même nature.

NOTE 5 Dans l'ISQ, les symboles correspondant aux dimensions des grandeurs de base sont:

La dimension d'une grandeur Q est donc notée dim Q = L^αM^βT^γI^δΘ^εN^ζJ^η où les exposants, appelés exposants dimensionnels, sont positifs, négatifs ou nuls.

1 Grandeurs et unités

• 1.1 grandeur
• 1.2 nature de grandeur
• 1.3 système de grandeurs
• 1.4 grandeur de base
• 1.5 grandeur dérivée
• 1.6 Système international de grandeurs
• 1.7 dimension
• 1.8 grandeur sans dimension
• 1.9 unité de mesure
• 1.10 unité de base
• 1.11 unité dérivée
• 1.12 unité dérivée cohérente
• 1.13 système d'unités
• 1.14 système cohérent d'unités
• 1.15 unité hors système
• 1.16 Système international d'unités
• 1.17 multiple d'une unité
• 1.18 sous-multiple d'une unité
• 1.19 valeur d'une grandeur
• 1.20 valeur numérique
• 1.21 algèbre des grandeurs
• 1.22 équation aux grandeurs
• 1.23 équation aux unités
• 1.24 facteur de conversion entre unités
• 1.25 équation aux valeurs numériques
• 1.26 grandeur ordinale
• 1.27 échelle de valeurs
• 1.28 échelle ordinale
• 1.29 échelle de référence conventionnelle
• 1.30 propriété qualitative

2 Mesurages

• 2.1 mesurage
• 2.2 métrologie
• 2.3 mesurande
• 2.4 principe de mesure
• 2.5 méthode de mesure
• 2.6 procédure de mesure
• 2.7 procédure de mesure de référence
• 2.8 procédure de mesure primaire
• 2.9 résultat de mesure
• 2.10 valeur mesurée
• 2.11 valeur vraie
• 2.12 valeur conventionnelle
• 2.13 exactitude de mesure
• 2.14 justesse de mesure
• 2.15 fidélité de mesure
• 2.16 erreur de mesure
• 2.17 erreur systématique
• 2.18 biais de mesure
• 2.19 erreur aléatoire
• 2.20 condition de répétabilité
• 2.21 répétabilité de mesure
• 2.22 condition de fidélité intermédiaire
• 2.23 fidélité intermédiaire de mesure
• 2.24 condition de reproductibilité
• 2.25 reproductibilité de mesure
• 2.26 incertitude de mesure
• 2.27 incertitude définitionnelle
• 2.28 évaluation de type A de l'incertitude
• 2.29 évaluation de type B de l'incertitude
• 2.30 incertitude-type
• 2.31 incertitude-type composée
• 2.32 incertitude-type relative
• 2.33 bilan d'incertitude
• 2.34 incertitude cible
• 2.35 incertitude élargie
• 2.36 intervalle élargi
• 2.37 probabilité de couverture
• 2.38 facteur d'élargissement
• 2.39 étalonnage
• 2.40 hiérarchie d'étalonnage
• 2.41 traçabilité métrologique
• 2.42 chaîne de traçabilité métrologique
• 2.43 traçabilité métrologique à une unité de mesure
• 2.44 vérification
• 2.45 validation
• 2.46 comparabilité métrologique
• 2.47 compatibilité de mesure
• 2.48 modèle de mesure
• 2.49 fonction de mesure
• 2.50 grandeur d'entrée dans un modèle de mesure
• 2.51 grandeur de sortie dans un modèle de mesure
• 2.52 grandeur d'influence
• 2.53 correction

3 Dispositifs de mesure

• 3.1 instrument de mesure
• 3.2 système de mesure
• 3.3 appareil de mesure indicateur
• 3.4 appareil de mesure afficheur
• 3.5 échelle d'un appareil de mesure afficheur
• 3.6 mesure matérialisée
• 3.7 transducteur de mesure
• 3.8 capteur
• 3.9 détecteur
• 3.10 chaîne de mesure
• 3.11 ajustage d'un système de mesure
• 3.12 réglage de zéro

4 Propriétés des dispositifs de mesure

• 4.1 indication
• 4.2 indication du blanc
• 4.3 intervalle des indications
• 4.4 intervalle nominal des indications
• 4.5 étendue de mesure
• 4.6 valeur nominale
• 4.7 intervalle de mesure
• 4.8 condition de régime établi
• 4.9 condition assignée de fonctionnement
• 4.10 condition limite de fonctionnement
• 4.11 condition de fonctionnement de référence
• 4.12 sensibilité
• 4.13 sélectivité
• 4.14 résolution
• 4.15 résolution d'un dispositif afficheur
• 4.16 seuil de discrimination
• 4.17 zone morte
• 4.18 limite de détection
• 4.19 stabilité
• 4.20 biais instrumental
• 4.21 dérive instrumentale
• 4.22 variation due à une grandeur d'influence
• 4.23 temps de réponse à un échelon
• 4.24 incertitude instrumentale
• 4.25 classe d'exactitude
• 4.26 erreur maximale tolérée
• 4.27 erreur au point de contrôle
• 4.28 erreur à zéro
• 4.29 incertitude de mesure à zéro
• 4.30 diagramme d'étalonnage
• 4.31 courbe d'étalonnage

5 Étalons

• 5.1 étalon
• 5.2 étalon international
• 5.3 étalon national
• 5.4 étalon primaire
• 5.5 étalon secondaire
• 5.6 étalon de référence
• 5.7 étalon de travail
• 5.8 étalon voyageur
• 5.9 dispositif de transfert
• 5.10 étalon intrinsèque
• 5.11 conservation d'un étalon
• 5.12 . . .
• 5.13 matériau de référence
• 5.14 matériau de référence certifié
• 5.15 commutabilité d'un matériau de référence
• 5.16 donnée de référence
• 5.17 donnée de référence normalisée
• 5.18 valeur de référence